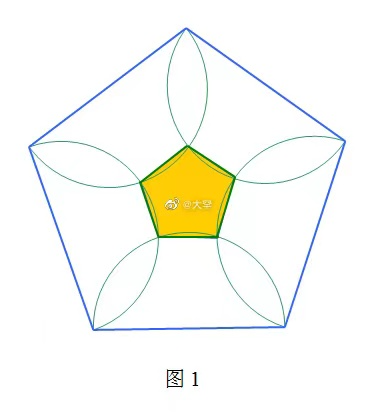
如图1，两个正五边形和五个半圆，求蓝色区域（大正五边形）与橙色区域（小正五边形）面积之比.
【大罕解答】
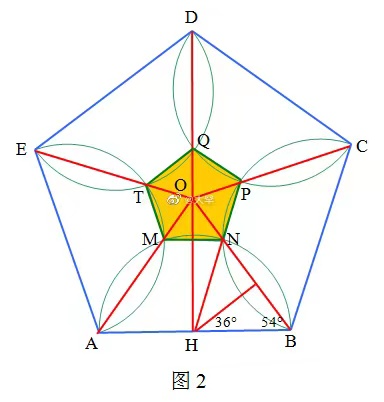
正五边形ABCDE、MNPQT有共同的中心O，设AB=a，
作DH⊥AB于H，由对称性可知点Q、O均在DH上，且P、N、H三点共线，PH//BC，如图2，
在△BHN中，∠BHN=72°，
∴BN=asin36°，
又OB=a/(2sin36°)，
∴ON/OB=(OB-BN)/OB
=1-BN/OB=1-2(sin36°)^2=cos72°
=(√5-1)/4，
∴S(ABCDE)/S(MNPQT)=(OB/ON)^2
=[4/(√5-1)]^2 =(√5+1)^2
=4φ^2，
其中(1+√5)/2.
【评论】以正五边形的各边为直径向内作半圆，诸交点得到小的正五边形，这就是“母子正五边形”。这是一个非常优美的图形！
正五边形的角大都涉及到18°系列，36°、54°、72°、108°，这些角往往与“黄金分割”有关。这又是一个迷人的地方。
1
555
1
1
1
1
1
1
1
1
1
1
1
555
1
1
1
1
1
555
1
1
1
1
1
1
1
1
555
1
1
1
1
1
1
1
1
555
1
1
1
1
1
1
555
1
1
1
1
1
1
1
1
555
1
1
1
1
1
1
1
555