蚂蚁环游-几何趣题
最近遇到2道蚂蚁环游的几何趣题,很有意思。
数学##概率##期望##数学竞赛##数学挑战##马尔可夫过程
看很多算这个还比较复杂,我的常规的简单解法以及巧妙的几秒钟解法。
我的方法最后把离散随机过程巧妙等效的转换成了电路图的求电流和电阻电压了。
网友投稿询问一道题,觉得很有意思,其实这是一个特殊情形的马尔科夫问题。马尔科夫解法更通用,但是很复杂以及没有利用到这个转移概率分布的概率的一些特性。
这解法更初等一般人更容易看明白,特别是回到原点的解,异常简单。
当然马尔可夫解法是最本质最通用的解法,可以得到随机事件的每一步过程,涉及到矩阵的一些概念以及运算很复杂,一般人也很难理解。
常见大家的解法是列线形方程组,我的巧妙的解法其实是巧妙的解释了这个线性方程组以及等效的巧解了这个线性方程组。这些都是只对最终的期望值这个均值做了求解。
问题:
一蚂蚁沿着简单多面体(或者平面连通图)的边爬行,若到达一顶点,则平均随机选连接这个顶点的一边继续爬,包含爬过来的边。
蚂蚁最开始从某顶点O出发,随机乱爬,若路径碰巧返回到O点,就停止爬行。
问蚂蚁爬行全程经过顶点次数的数学期望值?出发和终止O点只算一次,中间只要经过一次顶点就算一次,或者相当于每条边都算距离1,计算爬行的长度的期望值。
网友问的是正12面体,我直接任意连通图求解。
解:
假设从某点A出发,第n步到达O点的概率为pn,那么期望值f(0)= ∑pn*n,封闭联通图,最终所有都会到达终点,有∑pn=1。
如果已经m步到达A再出发,那么到达O点的步数都延后m步,所以期望值
f(m)= ∑pn(n+m)= ∑pnn+ ∑pn*m=m+f(0) (1)
其实有更一般的结果,m步概率p在A点,出发到达O点的步数期望值:
f(p,m)=pf(1,m)=p ∑pn(n+m)=p( ∑pnn+ ∑pnm)=p(m+c)。
显然期望值对于起点步数线性。如果没有这一步直接得到(2)其实是有点缺乏严密性的,这一步很多直接用但是这一步不是太显然。
O点标记为第一点。设平面图顶点An出发到顶点O的距离期望值是an,顶点An的边是bn,O点出发再到O点的长度期望值是x。
对于O点a1=0
对于其它点An有:
an=1/bn ∑fk(1)=1+1/bn∑ak,(2)所有和An相连的顶点求和。
有了(1),得到(2)更好理解。
a1=0
an=1+1/bn*∑ak。
x=1+1/b1*∑ak。
求解这个线形方程组,就得到任意点出发到达O的路径期望值了,x就是O点出发后回到O点路径期望值。大多数人到了这一步就老老实实的去解这个线性方程组就完事。
其实这个线形方程组,对于x还相当好求。
变形一下几个等式:
a1=0
bn*an=bn+∑ak (3)
b1*x=b1+∑ak
所有等式相加,除了未知数x以外,其它未知数抵消,
b1*x=∑bn=2E ,E为连通图的边数。
x=2E/b1
如果是正多面体,会有很简化的结果,得到,x=n,n顶点数。
惊叹于这个结果是这么简单漂亮,觉得应该有更通用简单的原因,于是试图寻找更简单更通用的解法。这也是我解题习惯于先用痛用未知数的解法,而不是带入具体数据求解,这样更容易发现本质。很多解正方体或者正12面体得到x=8或者x=20就算完成。
思考后,对于这结果,好像找到一个直观的解释了也是一个秒解的妙解。
每个顶点bn只蚂蚁,O点有b1条边,每步有b1只蚂蚁进去,有b1只蚂蚁刚好出来。其它点也保持蚂蚁数不变。这样刚好维持平衡。这样每一步蚂蚁总共爬了2E的距离,b1只蚂蚁出来,那么一只蚂蚁就平均爬了x=2E/b1步。我简直是太聪明了,这么是秒算结果呀。
没想到问题结果是这么简单漂亮。现实正多面体只有简单的几个,其实连通图还有更多形式的正多面体,只要连接关系任意两点对称就行。
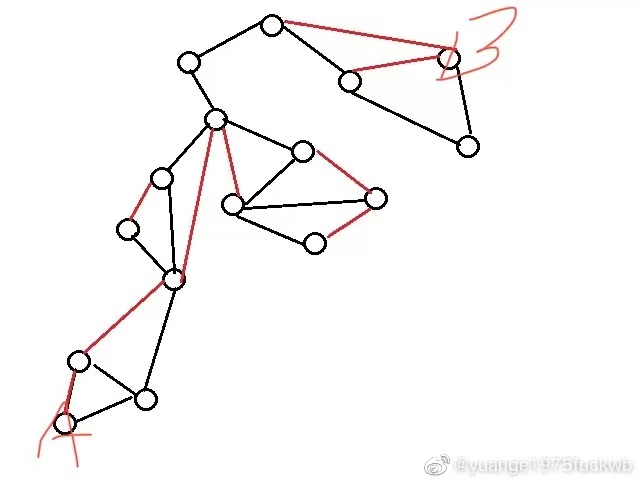
没理解方程的可以对照下图更好理解,下图A点就是O点。
解完x后,需求就是怎么快速口算解出所有未知数,就是任意两点的距离期望值。多一点未知数的线性方程组对于口算可基本上还是很难办到。
后记:
再思考后,猛然想到找到平衡点后,其实就是求平衡流量。这不就是一简单的电路图吗?
简单的就得到任意两点的a到b距离x(a,b):
连通图每条边的电阻为1欧姆,连接a点电源正级连接b点电源负级电压为0,b点电流为I,各顶点电压为un,边数为bn。那么有:
x(a,b)=1/I∑bnun (4)
想象每个顶点有bnun只电蚂蚁?,让每个顶点的蚂蚁沿着每条边bnun/bn=un只蚂蚁爬行一步,a点和b点都总爬出∑△ui=∑i1=I只蚂蚁,其它顶点蚂蚁数变化∑△ui=∑i1=0,将保持不变。
这样下一步a点补充I只蚂蚁,一直下去保持了稳定状态。I只蚂蚁每一步蚂蚁总共爬行了相同的距离∑bn*un ,那每只蚂蚁从a进到b出就平均爬行距离为
x(a,b)=1/I∑bnun 。
O点和O点的距离为0。如果O点进O点出,O点的边为b1,实际上就相当于1步后和O点连通距离为1的顶点都是接入电源正级,电源电压为1的话,这样就除了O点电压为0,其它电压都为un=1,O点电流为b1。x=1+1/b1∑bnun =1+1/b1*(2E-b1)=2E/b1。
简单的串并联电路和一些对称的电路图可以很好算电阻,电流和电压可以直接算出来,复杂不对称的串并联桥电路还是有点不好算电流电压。
如图2,简单的就可以口算v2到v4的距离期望值为x=(103+52+43+22)/21=8/3。
如图3,就算这样的复杂的A到B的路径期望值也很好口算x=(2+6+15+26+3416+373+382+395+436+472)/8。
对于中间有独立点的情形,就是联通图切段某点就分成了2个连通图,也可以分开算。(4)可以很简单的推导出:
x(a,b,c)=x(a,b)+x(b,c)+Vab*Rbc (5)
x(a,b,c)是a到c的距离,先经过b的独立点,x(a,b)是a到b的距离,一般不等于x(b,a),
x(b,c)是切断a到b后b到c的距离,b要包含其所有边,
Vab是a到b不包含b的顶点数,
Rbc是b到c的电阻,按每条边1欧姆算。
对于图3这种有部分电路电阻不是整数的情形,可以算电流I=1的情形,(5)这样分开算更适合口算。等于把整数和分数分开了相加,I=1整数会变小更适合相加,分数很多就成了相同的分数,算个数相乘也很适合口算。
再后续:
这算是一类特殊转移概率的马尔可夫过程,如果转移概率不是每边都是相同概率呢?
一般的是:
an=1+∑pk*ak,∑pk=1。巧解的就是一般常见的特殊情形pk=1/bn都相等的这类型。
也可以常规办法解线形方程组。
下一步看看这种基本的问题能不能同样有巧妙方法解决。

评论已关闭